INTRODUÇÃO AOS ALGORITMOS

1. DEFINIÇÃO

1. TIPOS DE ALGORITMOS

            Existem diversos tipos de algoritmos. Dentre eles podemos citar o pseudocódigo, a descrição narrativa e o fluxograma.

            O Pseudocódigo utiliza linguagem estruturada e se assemelha na fórmula, a um programa escrito em Pascal que é também chamado de Português Estruturado (Portugol). Geralmente baseia-se em uma PDL (Program Design Language – Linguagem de Projeto de Programação).

            A Descrição Narrativa utiliza a linguagem natural para especificar os passos para a realização de tarefas.

            O Fluxograma é uma forma universal de representação, pois se utiliza de figuras geométricas para ilustrar os passos a serem seguidos para a resolução dos problemas. É uma forma simbólica usada pelos programadores no esboço e desenvolvimento de programas. Ele é uma ferramenta usada e desenvolvida com a finalidade de descrever o fluxo de ação de um determinado trabalho lógico, seja manual ou mecânico, especificando os suportes usados para os dados e para as informações.

2. O FLUXOGRAMA

            Cada ação executada dentro de um Fluxograma recebe símbolos que permitem ao usuário, bem como ao programador ou profissional, seguir passo a passo a resolução de um problema.

2.1. PRINCIPAIS SIMBOLOGIAS

1. TIPOS DE INFORMAÇÃO

            É necessário considerar que um computador nada mais é do que uma ferramenta utilizada para solucionar problemas que envolvam a manipulação de informações, sendo que essas informações classificam-se a grosso modo em dois tipos básicos: dados e instruções.

1.1.        TIPOS DE DADOS

            Os dados são representados pelas informações a serem tratadas (processadas) por um computador. Essas informações estão caracterizadas por três tipos de dados, a saber: dados numéricos (inteiros e reais), dados caracteres e dados lógicos.

·        TIPOS INTEIROS: são caracterizados como tipos inteiros os dados numéricos positivos ou negativos, excluindo-se destes qualquer número fracionário ou decimal. Como exemplo deste tipo de dado têm-se os valores: 35, 0, -56, entre outros.

·        TIPOS REAIS: são caracterizados como tipos reais os dados numéricos positivos, negativos e números fracionários e decimais. Como exemplo deste tipo de dado têm-se os valores: 35; 0; 1; -56; 1.3; -45.897; 1.84467440737096E19; entre outros.

·        TIPOS CARACTERES: são caracterizadas como tipos caracteres as sequências contendo letras, números e símbolos especiais. Uma sequência de caracteres deve ser indicada entre aspas (“”). Este tipo de dado é também conhecido como: alfanumérico, string, literal ou cadeia. Como exemplo deste tipo de dado, tem-se os valores: “PROGRAMAÇÃO”, “Rua Alfa, 52 Ap.1”, “Fone: 574-9988”, “04387-456”, “ “, “7”, entre outros valores.

·        TIPOS LÓGICOS: são caracterizados como tipos lógicos os dados com valores verdadeiro e falso, sendo que este tipo de dado poderá representar apenas um dos dois valores. Ele é chamado por alguns de tipo booleano, devido à contribuição do filósofo e matemático inglês George Boole na área da lógica matemática. Para facilitar a citação de um dado do tipo lógico, fica aqui declarado que estes deverão ser apresentados e delimitados pelo caractere (.). Como exemplo deste tipo de dado têm-se os valores: .Falso., .F. e .N. (para o valor lógico: falso) e .Verdadeiro., .V. e  .S. (para o valor lógico: verdadeiro).

1.2.        VARIÁVEIS

            Tem se como definição de variável tudo aquilo que é sujeito a variações, que é incerto, instável ou constantes. E quando se fala de computadores, temos que ter em mente que o volume de informações a serem tratadas é grande e diversificado. Desta forma, os dados a serem processados serão bastante variáveis.

            Todo dado a ser armazenado na memória de um computador deve ser previamente identificado, ou seja, primeiro é necessário saber qual o seu tipo para depois fazer o seu armazenamento adequado. Estando armazenado o dado desejado, ele poderá ser utilizado e manipulado a qualquer momento.

            Para utilizar o conceito de variável, imagine que a memória de um computador é um grande arquivo com várias gavetas, sendo que cada gaveta pode apenas armazenar um único valor (seja ele numérico, caractere ou lógico). Se for um grande arquivo com várias gavetas, você há de concordar que é necessário identificar com um nome a gaveta que se pretende utilizar. Desta forma o valor armazenado pode ser utilizado a qualquer momento.

            O nome de uma variável é utilizado para sua identificação e posterior uso dentro de um programa. Sendo assim, é necessário estabelecer algumas regras de utilização das variáveis:

·        Nomes de uma variável poderão ser atribuídos com um ou mais caracteres;

·        O primeiro caractere do nome de uma variável não poderá ser, em hipótese alguma, um número; sempre deverá ser uma letra;

·        O nome de uma variável não poderá possuir espaços em branco;

·        Não poderá ser nome de uma variável uma palavra reservada a uma instrução de programa;

·        Não poderão ser utilizados outros caracteres a não ser letras e números.

            São nomes válidos de variáveis: NOMEUSUARIO, FONE1, X, DELTA25, Z4, entre outros. São nomes inválidos de variáveis: NOME USUÁRIO, 1X, FONE#, ESCREVA (considerando que seja esta uma palavra reservada à instrução de uma linguagem, no caso, o nosso “português estruturado”).

            Devemos ainda considerar que dentro de um programa uma variável pode exercer dois papéis. Um de ação, quando é modificada ao longo de um programa para apresentar um determinado resultado, e o segundo de controle, a qual poderá ser “vigiada” e controlada durante a execução de um programa.

1.3.        CONSTANTES

            Tem-se como definição de constante tudo aquilo que é fixo ou estável. E existirão vários momentos em que este conceito deverá estar em uso. Por exemplo, o valor 1.23 da fórmula seguinte é uma constante: RESULTADO = ENTRADA*1.23.

1.4.        OS OPERADORES ARITMÉTICOS

            Tanto variáveis como constantes poderão ser utilizadas na elaboração de cálculos matemáticos, ou seja, na elaboração de expressões aritméticas, desde que sejam estabelecidas como do tipo real ou inteiro, e para que isto ocorra é necessária a utilização de operadores aritméticos.

            Os operadores aritméticos são classificados em duas categorias, sendo binários ou unários. São binários quando atuam em operações de exponenciação, multiplicação, divisão, adição e subtração. São unários quando atuam na inversão de um valor, atribuindo a este o sinal positivo ou negativo. Veja em seguida, a tabela de prioridade matemática existente quanto à utilização destes operadores:

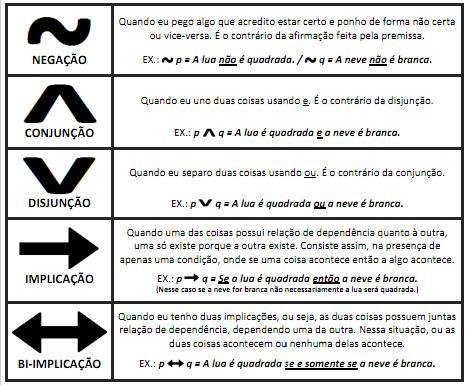
 1.5.        OS OPERADORES LÓGICOS

4.6.        AS EXPRESSÕES ARITMÉTICAS OU FÓRMULAS MATEMÁTICAS

            Será muito comum em programação o uso de expressões aritméticas ou fórmulas matemáticas, uma vez que a maior parte do trabalho computacional está relacionado e envolve a utilização de cálculos. Estas expressões são definidas pelo relacionamento existente entre variáveis e constantes numéricas por meio da utilização dos operadores aritméticos.

            As expressões aritméticas em computação são escritas de uma forma um pouco diferente da forma conhecida em matemática, por exemplo, a expressão X = {43. [55: (30+2)]} será escrita na forma computacional como X <- (43* (55/ (30+2))).

            Perceba que as chaves e colchetes são abolidos, utilizando-se em seu lugar apenas os parênteses. É também substituído o sinal de (=) igual pelo sinal de (¬ também representado pela junção do sinal de maior que (<) com o sinal de menos (-) resultando: <-) implicado ou atribuído.

            O sinal implicado ou atribuído (<-) é utilizado para indicar que o valor de uma expressão aritmética ou fórmula matemática está sendo armazenado em uma variável.

1.2.        INSTRUÇÕES BÁSICAS

            As instruções são representadas pelo conjunto de palavras-chave (vocabulário) de uma determinada linguagem de programação, que tem por finalidade comandar em um computador o seu funcionamento e a forma como os dados armazenados deverão ser tratados. É importante saber que existem diferentes linguagens de programação e por isso é claro que existem diferentes formas de se escrever uma mesma instrução de acordo com a linguagem utilizada.

            Nesta apostila usaremos uma pseudolinguagem denominada por uns de Portugol que será empregada em um software usado para interpretar algoritmos e empregado na aprendizagem lógica da programação, este programa será o VisualG e seguem abaixo as principais instruções que serão utilizadas inicialmente:

INTRODUÇÃO À LÓGICA DE PROGRAMAÇÃO

1. DEFINIÇÕES

1.1.        LÓGICA

Coerência de raciocínio e de idéias; É o modo de raciocinar peculiar a alguém, ou a um grupo; Sequência coerente, regular e necessária de acontecimentos, de coisas; É a ciência dos princípios normativos e formas de raciocínio; Encadeamento, aparentemente lógico, de juízos ou pensamentos, capacidade de pensar, refletir e considerar; É aquilo que é conseguido através do raciocínio e pensamento.

A lógica foi desenvolvida por Aristóteles (Filósofo Antigo), discípulo de Platão que era discípulo de Sócrates, assim, pode-se dizer que um sofreu influências do outro: Platão absorveu toda a teoria de Sócrates e Aristóteles absorveu toda a teoria de Platão.

1.2.        PROGRAMAÇÃO

Conjunto de apresentações, ações, eventos, etc. planejados antecipadamente; ciência ou técnica de elaboração de programas de computador; Técnicas para resolução de um problema.

 

2. OBJETIVOS E PRINCÍPIOS DA LÓGICA MATEMÁTICA

“Desenvolver a capacidade de encadeamento de idéias numa sequência lógica através das técnicas e do desenvolvimento de aplicações em uma linguagem”.

           
            O principal objetivo da lógica matemática é encontrar a validade dos argumentos.

·        ARGUMENTO: Parte que compõe a sequência até chegar a um resultado.

·        PREMISSA: Princípio que dá base a uma conclusão.

·        PROPOSIÇÃO: Estrutura linguística composta por sujeito e predicado.

Mas como eu posso saber se a minha proposição é verdadeira?

R: Analisando as premissas (proposições) numa operação lógica.

Na matemática é comum efetuarmos operações que fazem uso de números, incógnitas e operadores. Na lógica isso é semelhante, usaremos ao invés de números e incógnitas (que representam valores numéricos) algo que chamamos de variável.

·        VARIÁVEL: letra latina minúscula que representa aquilo que eu quero dizer (no caso minhas premissas e proposições) e que serve para indicar as fórmulas.

P = A lua é quadrada.

q = A neve é branca.

Para unir as premissas (variáveis) é necessário o uso de conectivos. Os principais são os seguintes:

1. TABELA VERDADE

            É um recurso utilizado por programadores iniciantes para entender melhor a lógica inicial de qualquer programa, ela se baseia no uso das variáveis, operadas por conectivos lógicos resultando e contendo apenas dois valores, que podem ser verdadeiro (V) ou falso (F).

3.1. NEGAÇÃO

            Nela se o valor da variável é verdadeiro o resultado da operação será falso e se for falso será verdadeiro, em outras palavras, o resultado será sempre o oposto do valor assumido pela variável.

     3.2. CONJUNÇÃO

Nela o resultado só é verdadeiro se o valor das duas variáveis for verdadeiro, caso um ou os dois valores forem falsos a operação resulta falsa.

      3.3. DISJUNÇÃO

Nela o resultado é visualmente o oposto do que acontece na conjunção, ele só é falso quando o valor das duas variáveis é falso, caso um ou os dois valores forem verdadeiros a operação resulta verdadeira. Para facilitar pode-se auto-questionar quanto a preferência lógica, ou seja: entre verdadeiro e falso o que é melhor? É lógico que o melhor será sempre o verdadeiro, portanto sempre que eu tiver esta opção o resultado será verdadeiro.

3.4. IMPLICAÇÃO

Nela o resultado só é falso quando o valor da primeira variável for verdadeiro e o da última falso, nos demais casos (Ambas verdadeiras; a primeira falsa e a segunda verdadeira; e ambas falsas resultam verdadeiras).

 3.5.        BI-IMPLICAÇÃO

Nela se houver em qualquer situação uma variável de valor verdadeiro e uma de valor falso (ou seja, variáveis de valor diferente), a operação resulta falsa, enquanto que se ambas as variáveis forem verdadeiras, ou ambas forem falsas o resultado é verdadeiro. De forma mais simples, valores iguais resultam verdadeiro e valores diferentes resultam falso.

3.6. OPERAÇÕES COM CONECTIVOS LÓGICOS

·        PARENTESES: servem para denotar o alcance da minha operação.

·        VALORES: Nesse caso, podem ser VERDADEIRO (V) e FALSO (F).

            A princípio, é preciso saber construir a nossa tabela de operação lógica, para isso é preciso determinar o número de linhas (que está relacionado com o número de possíveis combinações entre as variáveis), para isso usa-se a seguinte fórmula:

            Onde: NL = Número de Linhas; NVL = Número de Valores; e NVR = Número de Variáveis.

EX.:

a)     ((p  q)    p)

Valores possíveis: (V) ou (F); Variáveis: (p) e (q);

NL = NVL^NVR = 2² = 4 linhas.