INTRODUÇÃO À LÓGICA DE PROGRAMAÇÃO

1. DEFINIÇÕES

1.1.        LÓGICA

Coerência de raciocínio e de idéias; É o modo de raciocinar peculiar a alguém, ou a um grupo; Sequência coerente, regular e necessária de acontecimentos, de coisas; É a ciência dos princípios normativos e formas de raciocínio; Encadeamento, aparentemente lógico, de juízos ou pensamentos, capacidade de pensar, refletir e considerar; É aquilo que é conseguido através do raciocínio e pensamento.

A lógica foi desenvolvida por Aristóteles (Filósofo Antigo), discípulo de Platão que era discípulo de Sócrates, assim, pode-se dizer que um sofreu influências do outro: Platão absorveu toda a teoria de Sócrates e Aristóteles absorveu toda a teoria de Platão.

1.2.        PROGRAMAÇÃO

Conjunto de apresentações, ações, eventos, etc. planejados antecipadamente; ciência ou técnica de elaboração de programas de computador; Técnicas para resolução de um problema.

 

2. OBJETIVOS E PRINCÍPIOS DA LÓGICA MATEMÁTICA

“Desenvolver a capacidade de encadeamento de idéias numa sequência lógica através das técnicas e do desenvolvimento de aplicações em uma linguagem”.

           
            O principal objetivo da lógica matemática é encontrar a validade dos argumentos.

·        ARGUMENTO: Parte que compõe a sequência até chegar a um resultado.

·        PREMISSA: Princípio que dá base a uma conclusão.

·        PROPOSIÇÃO: Estrutura linguística composta por sujeito e predicado.

Mas como eu posso saber se a minha proposição é verdadeira?

R: Analisando as premissas (proposições) numa operação lógica.

Na matemática é comum efetuarmos operações que fazem uso de números, incógnitas e operadores. Na lógica isso é semelhante, usaremos ao invés de números e incógnitas (que representam valores numéricos) algo que chamamos de variável.

·        VARIÁVEL: letra latina minúscula que representa aquilo que eu quero dizer (no caso minhas premissas e proposições) e que serve para indicar as fórmulas.

P = A lua é quadrada.

q = A neve é branca.

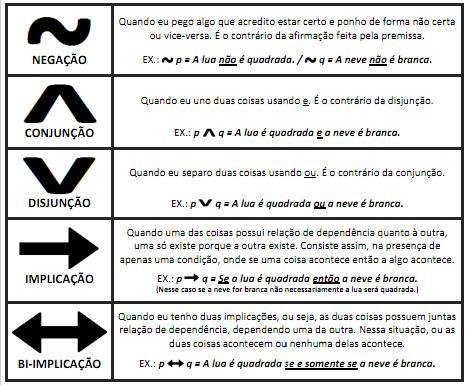
Para unir as premissas (variáveis) é necessário o uso de conectivos. Os principais são os seguintes:

1. TABELA VERDADE

            É um recurso utilizado por programadores iniciantes para entender melhor a lógica inicial de qualquer programa, ela se baseia no uso das variáveis, operadas por conectivos lógicos resultando e contendo apenas dois valores, que podem ser verdadeiro (V) ou falso (F).

3.1. NEGAÇÃO

            Nela se o valor da variável é verdadeiro o resultado da operação será falso e se for falso será verdadeiro, em outras palavras, o resultado será sempre o oposto do valor assumido pela variável.

     3.2. CONJUNÇÃO

Nela o resultado só é verdadeiro se o valor das duas variáveis for verdadeiro, caso um ou os dois valores forem falsos a operação resulta falsa.

      3.3. DISJUNÇÃO

Nela o resultado é visualmente o oposto do que acontece na conjunção, ele só é falso quando o valor das duas variáveis é falso, caso um ou os dois valores forem verdadeiros a operação resulta verdadeira. Para facilitar pode-se auto-questionar quanto a preferência lógica, ou seja: entre verdadeiro e falso o que é melhor? É lógico que o melhor será sempre o verdadeiro, portanto sempre que eu tiver esta opção o resultado será verdadeiro.

3.4. IMPLICAÇÃO

Nela o resultado só é falso quando o valor da primeira variável for verdadeiro e o da última falso, nos demais casos (Ambas verdadeiras; a primeira falsa e a segunda verdadeira; e ambas falsas resultam verdadeiras).

 3.5.        BI-IMPLICAÇÃO

Nela se houver em qualquer situação uma variável de valor verdadeiro e uma de valor falso (ou seja, variáveis de valor diferente), a operação resulta falsa, enquanto que se ambas as variáveis forem verdadeiras, ou ambas forem falsas o resultado é verdadeiro. De forma mais simples, valores iguais resultam verdadeiro e valores diferentes resultam falso.

3.6. OPERAÇÕES COM CONECTIVOS LÓGICOS

·        PARENTESES: servem para denotar o alcance da minha operação.

·        VALORES: Nesse caso, podem ser VERDADEIRO (V) e FALSO (F).

            A princípio, é preciso saber construir a nossa tabela de operação lógica, para isso é preciso determinar o número de linhas (que está relacionado com o número de possíveis combinações entre as variáveis), para isso usa-se a seguinte fórmula:

            Onde: NL = Número de Linhas; NVL = Número de Valores; e NVR = Número de Variáveis.

EX.:

a)     ((p  q)    p)

Valores possíveis: (V) ou (F); Variáveis: (p) e (q);

NL = NVL^NVR = 2² = 4 linhas.